Spatial Reasoning Explained
Spatial Reasoning
Part 1 of 4Spatial Reasoning is a logical reasoning system that assumed entities located in space and have a spatial structure. Making machines that can perceive and understand space has always been a researcher’s dream. Our lives could be enhanced by their assistance; with the spatial intelligence of machines, we would have new methods of planning and navigation through spatial orientation.
[2024/10/05] We can listen to this article as a Podcast Discussion, which is generated by Google’s Experimental NotebookLM. The AI hosts are both funny and insightful.
images/spatial-reasoning-explained/Podcast_Spatial_Reasoning_Explained.mp3
Topics of Spatial Reasoning
Computer science involves a list of interesting topics that required spatial reasoning ability:
-
Artificial Intelligence - Our everyday concepts are populated with qualitative spatial description. Something is sitting next to something else. The description is usually fuzzy and imprecise, yet we can deduce some non-trivial conclusion. For example, a train is going west. If the station exit is closer to the south, where would we sit on the train in order to exit faster? This involved the spatial structure of the train and qualitative understanding of the direction that train is travelling.
-
Spatial Database - In addition to well-known numeric or character objects, the “spatial object “ is a popular extension to the collection of the “database objects”. When the data has a spatial attribute, for example a street address or a phone number, we could use the spatial proximity to calculate and deduce more info. We are designating a finite geometric representation and operation to these spatial entities.
-
Image Recognition - When an object appears in the visual field, it’s of great interest to image recognition application. The object usually occurred in a spatial context, for example, the snacks sitting on top of a table. The snacks are described geometrically and spatially to precisely pin-point their location and spatial occupation.
-
Linguistic Processing - In communication, information is usually accompany with a spatial context. For example, battlefield logistics rely on spatial optimization to locate the most strategically advantageous position. The method is described both verbally and visually on a map. As another example, when a person is lost, they can usually describe their spatial context in a fragmentary form. After listening to the description, we are able to reconstruct the context to spatially pinpoint where the lose person is located.
Spatial Logic
When we are looking at a logical system, we can evaluate formula \(A \land B\) by evaluating
the truth or falsity of the entities \(A\) and \(B\) separately. The \(\land\) acting as
an logical AND operator defined within the logical system, specified both
\(A\) and \(B\) must be true; then \(A \land B\) will evaluate to true. If \(A\) and \(B\) are both
spatial entities, we are extending the formula with a spatial structure determining if
\(A \land B\) in \(S\) is possible. If it is possible, evaluate \(A \land B\) can be true within the space \(S\).
Assume a set of spatial entities \(A=\{A_1, A_2, ..., A_n\}\) we can assert a spatial structure \(S\) will be true for set \(A\). We call this set \(A\) as the possible spatial configuration of \(S\). To put this definition into a concrete example; If we need to navigate from a location X to location Y on land, we would assume there is a road network structure that connects the two locations. We can see the set \(A=\{X, ..., Y\}\) and the road network connecting all elements of \(A\) will be \(S\).
Sometimes, the spatial context does not need to involve a spatial entity occupying a location. For example, the most familiar 2D Cartesian coordinate system is a spatial reference system. With a chosen origin, e.g. in 2D (0,0), all possibilities of location are laid out explicitly. If there is a spatial entity positioned in this 2D Cartesian coordinate system, we refer to the entity’s location by measuring from the chosen origin. We shall come back to the difference between implicit spatial location (topological relations) and explicit spatial location (geometrical relations) in future discussion. We shall assume we are referring to implicit spatial location (topological relations) in this article.
Puzzles that required Spatial Logic
“What does a system look like when it has spatial reasoning ability?” This is best answered by an example. By writing a Prolog program, we will illustrate the possibility of solving spatial logic puzzles automatically. The following is a typical spatial logic puzzle that is often found in puzzle books.
Solving Spatial Logic Puzzle
Five married couples live in houses shown on the map below.
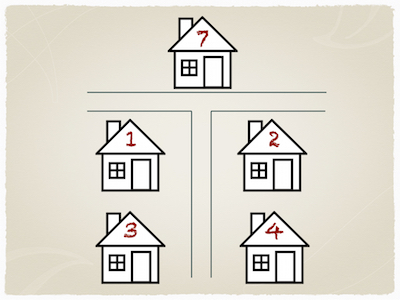
- Claire lives further east than Walter, who isn’t married to Mary.
- Walter lives further west than Debbie, who lives further south than Bill.
- Sandra lives further north than Katie, who lives further east than Adam.
- Lenny lives further north than Martin.
Thanks to Mihaela Malita,
we have the extremely useful
Prolog Puzzle Solving library.
We shall build our spatial puzzle solver in Prolog on top of bibmm.pl. Once the library has been downloaded, the program can be imported as (using SWI Prolog):
:-consult('bibmm.pl').
After careful analysis of the spatial configuration, we can code the following spatial structure. (Note: in order to save space, we put multiple Prolog statements into one line)
eastof(2,1). eastof(2,3). eastof(2,7). eastof(4,1).
eastof(4,3). eastof(4,7). eastof(7,1). eastof(7,3).
westof(1,2). westof(1,4). westof(1,7). westof(3,2).
westof(3,4). westof(3,7). westof(7,2). westof(7,4).
northof(7,1). northof(7,2). northof(7,3). northof(7,4).
northof(1,3). northof(1,4). northof(2,3). northof(2,4).
southof(1,7). southof(2,7). southof(3,7). southof(4,7).
southof(3,1). southof(4,1). southof(3,2). southof(4,2).
This is intentionally to enumerate all possible topological relations in this puzzle’s spatial structure. We shall improve with the spatial logic system later.
With the definition of the spatial structure, we can proceed to write the Prolog program to encode all the puzzle constraints, e.g. in our example, we have the list of 4 constraint statements. By breaking down each constraint statement carefully, we shall obtain the basic logic statement, either spatially or non-spatially constraints.
% include the facts of spatial structure
house([1,2,3,4,7]).
husband([adam,bill,lenny,martin,walter]).
wife([claire,debbie,katie,mary,sandra]).
start(Sol):- husband(M),wife(F),house(H),
Sol=[[M1,W1,H1],[M2,W2,H2],[M3,W3,H3],[M4,W4,H4],[M5,W5,H5]],
set_equal([H1,H2,H3,H4,H5],H),
% 1. Claire lives further east than Walter, who isn't married to Mary.
eastof(X1,X2),
member([_,claire,X1],Sol),
member([walter,_,X2],Sol),
member([_,mary,X3],Sol),
X2 \= X3,
% 2. Walter lives further west than Debbie, who lives further south than Bill.
member([_,debbie,X4],Sol),
westof(X2,X4),
member([bill,_,X5],Sol),
southof(X4,X5),
% 3. Sandra lives further north than Katie, who lives further east than Adam.
member([_,sandra,X6],Sol),
member([_,katie,X7],Sol),
northof(X6,X7),
member([adam,_,X8],Sol),
eastof(X7,X8),
% 4. Lenny lives further north than Martin.
member([lenny,_,X9],Sol),
member([martin,_,X10],Sol),
northof(X9,X10),
set_equal([M1,M2,M3,M4,M5],M),
set_equal([W1,W2,W3,W4,W5],W),
!.
How to run with swipl:
?- ['house'].
?- start(Sol), write_list(Sol), fail.
After executing the Prolog program, the puzzle’s solution will be revealed as,
[walter,sandra,1]
[lenny,debbie,2]
[adam,mary,3]
[martin,katie,4]
[bill,claire,7]
Just in case you don’t now how to exit from swipl:
?- halt.
Improved Spatial Relations Encoding
In the example, we have encoded the spatial structure via their topological relations by enumerating all possible pairwise relationship. This is not a very intelligent encoding scheme, and downright exhaustive. Smart readers will immediately notice, with our spatial intelligence, we have a set of spatial logic that can be applied.
For example,
eastof(2,1).
westof(1,2).
We can see the relations eastof and westof are symmetrical relation,
such that we know eastof(X,Y) immediately implies westof(Y,X) by spatial symmetry.
Therefore, without encoding all the symmetrical spatial relations, we could enter a logical rule as,
westof(X,Y) :- eastof(Y,X).
Then, we don’t need to encode any westof relations because westof
can be deduced from the symmetric eastof relation.
Similarly, we can put,
southof(X,Y) :- northof(Y,X).
Then, we don’t need to encode any southof relations because southhof
can be deduced from the symmetric northof relation.
The set of spatial relations are reduced to encode only eastof and northof relations.
eastof(2,1). eastof(2,3). eastof(2,7). eastof(4,1).
eastof(4,3). eastof(4,7). eastof(7,1). eastof(7,3).
northof(7,1). northof(7,2). northof(7,3). northof(7,4).
northof(1,3). northof(1,4). northof(2,3). northof(2,4).
How about the transitive relations? We can reduce northof relations by
only encoding the direct northof entities. And let the transitive
logical rule taking care of the implicit spatial relationship.
northof(X,Y) :-
X \= Y,
northof(X,Z),
northof(Z,Y).
Finally, we can refine the spatial relations to this reduced set,
by dropping the northof(7,3) and northof(7,4) indirect northof relations.
eastof(2,1). eastof(2,3). eastof(2,7). eastof(4,1).
eastof(4,3). eastof(4,7). eastof(7,1). eastof(7,3).
northof(7,1). northof(7,2).
northof(1,3). northof(1,4). northof(2,3). northof(2,4).
Spatial Reasoning is a Logical System
We have illustrated spatial reasoning with a topological language written in Prolog. The spatial entities are implicitly represented as a symbol, in this case, a house number. Alternatively, we can take the route of encoding the spatial entities explicitly by their geometric properties, and then calculating their spatial relations according to the geometric rules of the compass’s cardinal directions. Through this method, the set of topological relations can be generated instead of relying solely on hand coding.
Spatial reasoning is a strategy meant to deduce spatial truth in a logical system. We’re entering the domain of classical logic reasoning, where an object is limited to spatial entity. The rules of reasoning are governed by spatial logic; as a result, a wealth of literatures can be referenced and studied in this area. A good starting point is “The Handbook of Spatial Logics” by Marco Aiello et al..
The spatial logic overlay a structure of possibilities, in which many non-logical spatial situation can quickly be eliminated. This structure is the working premise of spatial validity. We need to follow the strict logical rules of spatial formulas, including the symmetric and transitive spatial rules as illustrated in this article. The indirect spatial relations can be deduced logically. The spatial relation is not necessarily just a simple “compass” rule in which only direction is described. Spatial relation can be generated by any computational geometry, such as convex hull or intersections, allowing for a wider range of spatial reasoning abilities. By understanding this foundation, you may find spatial reasoning to be applicable in many areas of your life, building up a newfound interest in this topic.
References
UPDATE 2020/09/04 I finally woke up and discovered how to use the amazing clp(fd) - Constraint Logic Programming (Finite Domain) module. Interested reader should continue explore “Solving Puzzles using Constraint Logic Programming in Prolog”, which explains how to use clp(fd) to solve the three types of puzzles, (1) Cryptarithmetic Puzzle, (2) Logic Puzzle and (3) Spatial Logic Puzzle.





