Using Prolog to Solve Logic Puzzles

What is a logic puzzle?

Logic Puzzle is a very funny thing. We are all very interest to read and try our brains to solve 1 or 2 of these puzzles. We thought that would improve our brain power after proving that we are logical enough to solve these logic puzzles. Of course, we are having fun for doing that too. But does it really improve our brain function, or this simply shows our brain is incapable to handle logical jumps in large recipe, like 6 houses, 5 couples and 7 kinds of tea. Obviously, we can not hold such a large logical space in our head, 6 x 5 x 7 = 210 possible solutions in this case. We need to resort to use some external recording devices to help us organized the “vast” information. Through the process of elimination and the deductive reasoning, we would come to a possible answer.

[2024/10/05] We can listen to this article as a Podcast Discussion, which is generated by Google’s Experimental NotebookLM. The AI hosts are both funny and insightful.

images/using-prolog-to-solve-logic-puzzles/Podcast_Prolog_Logic_Puzzle.mp3

After you solve a few puzzles, the natural tendency of a computer scientist is, “why don’t we automated to solve these puzzles?” Of course, your computer scientist’s inclination is always right. After a few rough analysis, we can see the puzzles are a search problem. If we are dumb enough to try, we can exhaustively list all possible answers and go back to the list of constraints to test if any one of the answer will satisfy all of the constraints. If the answer produces no contradiction, we know we have the right answer. However, our hand and brain are usually too lazy to do this type of dumb search. The puzzle book producer helps with giving you a table of all combinations so that you can pretend to not doing a dumb search. You are actually writing down something to eliminate some obvious dumb choices. The logical combination table serves as a smarter-dumb search device. This makes us feel really good.

Here is the popular Grid Method using by many puzzle enthusiasts and available in magazines dedicated to the subject.

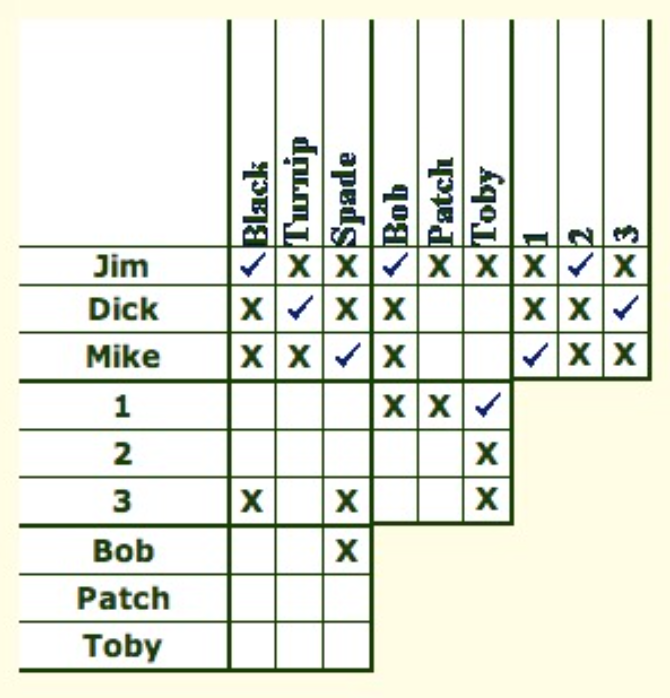
Putting those checkmarks to indicate something is possible or could be eliminated, that’s involve some language reading skills. If we could not reach a solution, we are not sure if we are reading all the English sentence properly after all. We would run through the original statements to verify if there is any contradictions in our possible solution.

Let’s be more serious, a computer scientist, when they are facing a logical problem, they would use a programming logics language, namely PRO-LOG, to tackle with the problem. This is a good idea until when you actually start to write some Prolog codes. You may ask, what is the problem? I said, did you actually try to do it. The problem is encoding a logic puzzle is more difficult than solving it. Luckily, the consequence of spending infinite amount of time to code is the expectation to solve the later problems faster. Under the amortization principle, we are coming out with a gain.

There is one professor in the world, Mihaela Malita takes it seriously enough to supply an extremely useful Prolog Puzzle Solving library. I am really thankful to her because it proves that automated puzzle solving is an interesting and a programming skills to have.

The Zebra Puzzle

The famous Zebra Puzzle comes with 15 facts and 2 questions: Who has a zebra and who drinks water?

The list of facts (or constraints):

1. There are 5 colored houses in a row, each having an owner, which has an animal, a favorite cigarette, a favorite drink.
2. The English lives in the red house.
3. The Spanish has a dog.
4. They drink coffee in the green house.
5. The Ukrainian drinks tea.
6. The green house is next to the white house.
7. The Winston smoker has a serpent.
8. In the yellow house they smoke Kool.
9. In the middle house they drink milk.
10. The Norwegian lives in the first house from the left.
11. The Chesterfield smoker lives near the man with the fox.
12. In the house near the house with the horse they smoke Kool.
13. The Lucky Strike smoker drinks juice.
14. The Japanese smokes Kent.
15. The Norwegian lives near the blue house.

We represent the houses as a list with 5 lists from left to right:

Sol = [[Man, Animal, Cigarette, Drink, Color], [..],[..],[..],[..] ]

We are using SWI Prolog to implement the zebra puzzle. Relying on the puzzle library bibmm.pl (download from Prolog Puzzle Solving library), we are translating the constraints into Prolog code as following,

:-consult('bibmm.pl').

start(Sol):- length(Sol,5),                 % 1
    member([english,_,_,_,red],Sol),        % 2
    member([spanish,dog,_,_,_],Sol),        % 3
    member([_,_,_,coffee,green],Sol),       % 4
    member([ukrainian,_,_,tea,_],Sol),      % 5
    right([_,_,_,_,green],[_,_,_,_,white], Sol),    % 6
    member([_,snake,winston,_,_],Sol),      % 7
    member([_,_,kool,_,yellow],Sol),        % 8
    Sol= [_,_,[_,_,_,milk,_],_,_],          % 9
        Sol= [[norwegian,_,_,_,_],_,_,_,_],         % 10
    next([_,_,chesterfield,_,_],[_,fox,_,_,_],Sol), % 11
    next([_,_,kool,_,_],[_,horse,_,_,_], Sol),  % 12
    member([_,_,lucky,juice,_],Sol),        % 13
    member([japonese,_,kent,_,_],Sol),      % 14
    next([norwegian,_,_,_,_],[_,_,_,_,blue],Sol),   % 15
    member([_,_,_,water,_],Sol),            % someone drinks water
    member([_,zebra,_,_,_],Sol).            % someone has a zebra

Then, we can execute the Prolog code to solve the zebra puzzle.

% swipl
?- ['zebra'].
?- start(Sol), write_list(Sol), fail.
[norwegian,fox,kool,water,yellow]
[ukrainian,horse,chesterfield,tea,blue]
[english,snake,winston,milk,red]
[japonese,zebra,kent,coffee,green]
[spanish,dog,lucky,juice,white]
false.
?- halt.

Programming to Solve Logic Puzzles

We shall analyze the thought process of how to solve the logic puzzle by writing a Prolog program. Here are the thoughts.

What are the Common Things Happening in Logic Puzzles?

For example, something is sitting next to something where something is a dog. We shall go ahead to find out a few of these.

The Zebra Puzzle mentioned above is more challenging: Additional background knowledge is required because the clues leave out some details, for example that houses are lined up in a row. Moreover, since the puzzle does not mention a zebra in the clues, it must be inferred that someone owns a zebra. These types of problems make clear that a representation is needed that also can be used to handle implicit assumptions which are present in natural language texts. Designing a computational system that is aimed at the precise understanding of natural language, we believe, requires that such interaction between semantic and background knowledge is taken seriously.

What are the Language Obstacles to Describe the Constraints?

For example, that exactly something seems to occur a lot of times. Your tongue will start to be tired after saying so many times about something next to something. You would confuse yourselves faster than describing the constraints.

What is the Optimal Representation of the States?

This is the problem of representation. Usually, the number of ways to represent the problem is a problem itself. Especially, you are trying to reach the “optimal” representation. This is true. With a smart representation, the solution could be easily seen. But with a bad representation, the solution is much more obscured.

The theory of vector representation is so generic that you can not know what it means until you find out how the vector’s schema is stating. For each field, there is a domain and the corresponding set of possible values. For in-between fields, there is a relation that string 2 or more fields together to provide their semantics. In term of processing, this is greatly convenience to use vector representation. To an interpreter of the system, this is like saying nothing but a set of symbols. Actually, this is not the problem of vector representation. This is the problem of the vector reader.

This is a great convenience to represent neighboring relationship between vector elements. Their relative position can be defined exactly as their neighboring relation, for example [A,B], such vector can indicate A is left-of B and B is right-of A, or simply A next-to B, B next-to A. Therefore, their index position is a logical space, where the relation can be established. This logical space does not imply metrical or regular. This is a conceptual space.

Such conceptual space does not require to be compacted. It can be a sparse representation of the connectedness. The metrical “distance” function has no definition. The “distance” may be the declarative “distance”. For example, A->B->C, where distance(A,B) is 1 and distance(A,C) is 2.

Why it is Interesting to Software Designer?

Let’s talk serious business, business specification is just like logic puzzle. How so? In the business domain, the constraints are usually preceived directly, something like a person who must have $1000 dollar before he could apply for credit card. However, a person who has $1000 may require some deductive reasoning to conclude. He may not have $1000 in an account directly. How about he has multiple accounts? or he has other collateral to cover this $1000 requirements. The smart business specification will list all of these deductive reasoning into a list of checks, or simply logics for software developer to code directly into the program.

With this in mind, I am very motivated to understand the mechanics of a logic puzzle. In a hope that could be used in business specification.

Search Problem and Intelligence

The logical space is a search tree, where all connectivity is represented as one logical deduction. For example, A->B, B->C, with the transitive rule, A->C. The business specification is hardly completed. There are many facts that is confirmed to be true. Some facts are relying on the logical deduction to make it.

What are the logical movements in the logical space?

• Representation of the search space
• Declarative programming in Prolog that used in logic puzzle
• Languages limitation
• Intelligence can be automated. You can answer questions with your business user.
• A method to explain the reasoning process, hidden assumptions and requirements.

It has been suggested to use logic puzzles as a test suite for computational systems that are able to answer questions based on a precise understand- ing of the natural language input. There are several benefits of using logic puzzles for evaluating natural language understanding systems. Most importantly, logic puzzles are created independently from the particular goals that are put on the agenda by researchers interested in natural language processing. To solve such puzzles, moreover, a computational system has to be able to handle a wide variety of linguistic phenomena and be able to reason with natural language input. Finally, logic puzzles define precise and well-structured problems, which set clear evaluation criteria for the performance of the computational system trying to solve such puzzles.

Logic grid puzzles, we believe, can provide us with an effective test for the quality of a formal representation. To solve logic puzzles, a formal representation is needed in order to represent semantic structure as well as the background knowledge. A precise understanding of text by a computational system will require a system that is able to map natural language input into the semantic representation and is able to reason with that input combined with any other available background knowledge (related to common-sense knowledge).

Three main reasons why logic grid puzzles are suitable for testing the quality of a formal representation.

1. To solve more complicated puzzles, a computational system must be able to handle quantifiers and scope, comparatives, tense, pronouns and anaphoric references, relative clauses, different types of adverbs, ordinals, etc.
2. Provide a basis for an incremental approach that aims at the gradual refinement of the representation language. That is, one can start with first-order logic to translate very simple puzzles, and add in subsequent steps additional features that allow the handling of anaphora, or events.
3. These puzzles are very well-structured and always come with a unique solution. The solution to a logic grid puzzle simply is the (unique) model that satisfies the natural language constraints.

Using Prolog for Real World

To know more about how Prolog could be used in real world problem, here are more suggested links to explore:

• http://stackoverflow.com/questions/130097/real-world-prolog-usage
• http://www.drdobbs.com/parallel/the-practical-application-of-prolog/184405220

References

UPDATE 2020/09/04 I finally woke up and discovered how to use the amazing clp(fd) - Constraint Logic Programming (Finite Domain) module. Interested reader should continue explore “Solving Puzzles using Constraint Logic Programming in Prolog”, which explains how to use clp(fd) to solve the three types of puzzles, (1) Cryptarithmetic Puzzle, (2) Logic Puzzle and (3) Spatial Logic Puzzle.